|
★ ★ ☆
<<< Precedente -
Successivo >>>
CONTENUTO DELLA PAGINA
Moto parabolico generale
Moto parabolico con partenza dall'origine
Il moto parabolico descrive il moto di un corpo soggetto lanciato con direzione orizzontale oppure obliqua, soggetto alla sola forza di gravità (si trascurano altre eventuali interazioni, come ad es. gli attriti). Infatti un corpo che si muove nello spazio, soggetto alla forza di gravità, subisce un'accelerazione costante verso il basso: se la velocità iniziale ha direzione verticale, il corpo segue un moto rettilineo uniformemente accelerato, mentre negli altri casi (direzione orizzontale oppure obliqua) segue una traiettoria parabolica, con asse di simmetria verticale e concavità verso il basso.
Il moto parabolico è la risultante della composizione di due moti: un moto rettilineo uniforme lungo una direzione orizzontale e un moto rettilineo uniformemente accelerato lungo una direzione verticale; infatti l'unica forza agente è quella di gravità, che a livello del mare produce un'accelerazione costante di circa 9,81 m/s², chiamata accelerazione di gravità (g) con direzione verticale e verso il basso.
Per studiare il moto parabolico è quindi conveniente utilizzare un sistema di riferimanto cartesiano avente come asse x la direzione orizzontale, in cui si studia il moto rettilineo uniforme, mentre come asse y la direzione verticale, in cui si studia il moto uniformemente accelerato avente come accelerazione g.
Moto parabolico generale
Nel caso generale di un corpo lanciato con direzione obliqua da un qualunque punto nel piano, il moto è descritto dalle seguenti equazioni:
Essendo:
- (x; y) le coordinate del punto nel piano cartesiano in un qualunque istante, ossia il vettore posizione;
- (x0; y0) le coordinate del punto all'istante iniziale, ossia il vettore posizione iniziale;
- v = (v X; v Y) il vettore velocità in un qualunque istante;
- v0 = (v0 X; v0 Y) il vettore velocità iniziale;
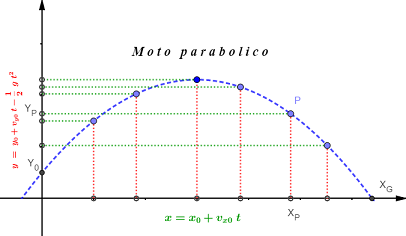Figura 1
In figura 1 è riportato una rappresentazione del moto parabolico in un classico piano cartesiano Oxy, in cui x0 = 0, quindi il corpo parte dall'asse y.
La Traiettoria, ossia la curva che percorre il punto nel piano cartesiano, è come abbiamo detto, a forma parabolica; l'equazione cartesiana di tale parabola è:
y = − g x² / 2(v0 X)² + (v0 Y)x / v0 X + y0.
^
Torna su
Moto parabolico con partenza dall'origine
Nel caso che un corpo parta dall'origine, con un angolo α rispetto all'asse x, allora:
- x0 = y0 = 0;
- v0 X = v0 cos(α);
- v0 Y = v0 sen(α).
Le equazioni diventano:
La Traiettoria in questo caso diventa più semplice:
y = − g x² / 2(v0 X)² + (v0 Y)x / v0 X.
Il Tempo di volo (𝒯) è il tempo impiegato a percorrere tutto l'arco di parabola interessato dal problema: dal punto di lancio fino al punto di atterraggio.
𝒯 = 2 v0 Y / g
La Gittata (xG) rappresenta l'ascissa del punto di caduta, ossia il punto in cui la traiettoria interseca l'asse x, e si calcola:
xG = 2 v0 X v0 Y / g.
Che si può anche scrivere:
xG = (v0)² sen(2α) / g.
La gittata dipende quindi dalla velocità iniziale e dall'angolo di lancio; si osserva che la gittata massima si ottiene con un'inclinazione di 45° rispetto all'asse x: infatti in tal caso otteniamo
xG = (v0)² sen(90°) / g = (v0)² / g.
Infine il punto più alto raggiunto dalla traiettoria rappresenta il vertice della parabola, e ha coordinate:
- posizione dell'altezza massima: xV = v0 X v0 Y / g
- altezza massima raggiunta: yV = (v0 Y)² / 2g
|
Esempio 5. Consiederiamo un proiettile sparato con una velocità iniziale di 20m/s in una direzione che forma un angolo di 30° con il piano orizzontale.
A quale altezza massima può arrivare e quale sarà la gittata?
Dati:
v0 = 20m/s
α = 30°
g = 9,81m/s²
xmax = incognita
ymax = incognita
Soluzione: osserviamo che il punto di massima altezza si può ottenere facilmente usando le formule del vertice; ma in alternativa può esser calcolato da zero anche in un altro modo: infatti corrisponde al punto nel quale la componente verticale delle velocità si annulla.
Per prima cosa scriviamo quindi le equazioni lungo la direzione x e la direzione y, considernado come punto di partenza l'origine degli assi:
|
ASSE X:
|
|
x (t) = (20m/s) · cos(30°) · t
v X (t) = (20m/s) · cos(30°)
|
|
ASSE Y:
|
|
y (t) = (20m/s) · sen(30°) · t − ½ (9,81m/s²) · t²
v Y (t) = (20m/s) · sen(30°) − (9,81m/s²) · t
|
Dobbiamo partire quindi dall'ultima formula, risolvendo l'equazione v Y (t) = 0.
(20m/s) · sen(30°) − (9,81m/s²) · t = 0
(20m/s) · 0,5 − (9,81m/s²) · t = 0
(10m/s) − (9,81m/s²) · t = 0
(9,81m/s²) · t = 10m/s
t = (10 / 9,81)s
t = 1,02s
A questo punto รจ sufficiente sostituire il valore trovato nell'equazione y(t), per trovare l'altezza al tempo t = 1.02s:
ymax = (20m/s)·sen(30°)·(1,02s) − ½(9,81m/s²)·(1,02s)²
ymax = (20m/s) · 0,5 · (1,02s) − (4,9m/s²) · (1,04s²)
ymax = (10,2m) − (5,1m)
ymax = 5,1m
Possiamo verificare i calcoli usando la formula:
yV = (v0 Y)² ⁄ 2g
con la quale arriviamo allo stesso risultato.
Analogamente anche per trovare la gittata possiamo usare la formula apposita, oppure usare il tempo trovato t = 1,02s
Infatti esso corrisponde a metà del tempo di volo, quindi:
𝒯 = 2,04s
Sostituendo 𝒯 nell'equazione della x, troviamo la gittata
xG = 20m/s cos(30°) · 2,04s
xG = 20m/s 0,87 · 2,04s
xG = 35,5 m.
Anche in questo caso possiamo verificare i calcoli usando la formula della gittata, con la quale arriviamo allo stesso risultato.
Conclusione: l'altezza massima raggiunta è di 5,1m e la gittata è di 35,5m.
|
^
Torna su
<<< Precedente -
Successivo >>>
|
