Introduzione - En. interna - 1° principio - Macchine termiche - 2° principio

★ ★ ☆

<<< Precedente   -   Successivo >>>

CONTENUTO DELLA PAGINA
Le macchine termiche
La macchina di Carnot

Le macchine termiche

Una 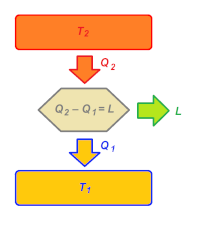macchina termica è un sistema che, sfruttando trasformazioni cicliche, riesce a produrre lavoro partendo dagli scambi di calore con l'ambiente esterno.

In particolare una macchina termica può esser schematizzata come un dispositivo inserito tra due sorgenti a temperature differenti e costanti, che dallo scambio di calore tra esse genera lavoro.

Come rappresentato in figura 2, abbiamo due sorgenti, quella calda in alto, a temperatura T₂ e quella fredda in basso, a temperatura T₁. Il calore ceduto dalla sorgete calda alla sorgente fredda passa attraverso la macchina, che ne sfrutta una parte per produrre lavoro; dettaglio:

• la sorgente calda cede alla macchina una quantità di calore Q₂;
• la macchina riceve dalla sorgente calda una quantità di calore Q₂ e cede alla sorgente fredda una quantità di calore Q₁, inferiore a quella ricevuta;
• la sorgente fredda riceve dalla macchina una quantità di calore Q₁.

In sintesi quindi:

Dal punto di vista della macchina, il calore Q₂ è positivo (in quanto assorbito), mentre il calore Q₁ è negativo (in quanto ceduto). Il calore in eccesso rimasto nella macchina viene convertito in lavoro:

Il modulo serve per considerare il valore assoluto di Q₁, a prescindere dal segno, e quindi far sì che di fatto il Lavoro si ottenga sempre da una sottrazione; inoltre, dal momento che Q₂ è maggiore di |Q₁|, il lavoro prodotto è positivo.

Una importante grandezza fisica che descrive l'efficacia di una macchina termica è il rendimento.

Il rendimento è un numero puro, non ha dimensioni, né unità di misura; assume sempre valori compresi tra 0 e 1; quanto maggiore è il rendimento, tanto migliore è l'efficacia di una macchina termica, poiché tanto maggiore sarà il lavoro compiuto dalla macchina.

Il rendimento si può calcolare anche nel modo equivalente:

^
Torna su

La macchina di Carnot

Una 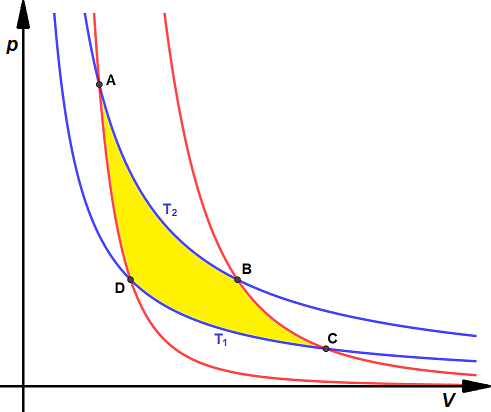macchina di Carnot è una macchina ideale, irrealizzabile nella realtà capace compiere una trasformazione ciclica con un ciclo reversibile su di un gas ideale.

Il ciclo di una macchina di Carnot, chiamato ciclo di Carnot è diviso in quattro fasi, come indicato in figura 3:

1. una espansione isotermica (linea blu AB)
2. una espansione adiabatica (linea rossa BC)
3. una compressione isotermica (linea blu CD)
4. una compressione adiabatica (linea rossa DA)

L'area gialla colorata all'interno del ciclo rappresenta il lavoro totale compiuto durante l'intero ciclo.

Studiamo il lavoro compiuto e il calore scambiato durante un ciclo di Carnot:

1. durante l'isotermica AB: L = Q = n RT₂ ln (𝒱_B ⁄ 𝒱_A)
2. durante l'adiabatica BC: L = n c_𝒱 (T₂ − T₁), mentre Q = 0;
3. durante l'isotermica CD: L = Q = n RT₁ ln (𝒱_D ⁄ 𝒱_C)
4. durante l'adiabatica DA: L = n c_𝒱 (T₁ − T₂), mentre Q = 0;

Il lavoro totale prodotto in un ciclo si ottiene sommando algebricamente i lavori durante le quattro trasformazioni. Possiamo osservare che esso dipende solo dalle due trasformazioni isoterme, in quanto le adiabatiche compiono due lavori opposti, che si annullano; inoltre, poiché vale la proporzione:

𝒱_B ⁄ 𝒱_A = 𝒱_C ⁄ 𝒱_D

allora il lavoro totale di un ciclo di Carnot può esser scritto:

Il calore assorbito dalla macchina (Q₂) corrisponde al calore prodotto nella trasformazione AB; mentre il calore ceduto (Q₁) corrisponde al quello della trasformazione CD; di conseguenza, facendo calcoli analoghi, si ottiene:

Da questi risultati si giunge all'osservazione che il rendimento η_R di una macchina reversibile, ed in particolare di una macchina di Carnot, si può calcolare anche con la seguente formula:

Il rendimento sarà massimo (uguale a 1) solamente nel caso non realizzabile in cui T₁ = 0K, ossia che la sorgente fredda sia allo zero assoluto.

Infine, un importantissimo risultato è il seguente:

Quindi il rendimento η di una qualunque macchina è minore o uguale al rendimento η_R di una macchina reversibile che lavori tra le stesse due temperature.

^
Torna su

<<< Precedente   -   Successivo >>>