Introduzione - Momento d'inerzia - Dinamica rotazionale - Tralazione e rotazione

★ ★ ☆

<<< Precedente   -   Successivo >>>

CONTENUTO DELLA PAGINA
Momento d'inerzia dei punti materiali
Momento d'inerzia dei corpi rigidi
Inerzia e rotazione

Momento d'inerzia dei punti materiali

Per spostare un corpo fermo, o per modificarne il moto, si deve applicare una forza; analogamente per modificare la rotazione di un corpo, si deve applicare un momento meccanico. Tuttavia ogni corpo oppone sempre una propria resistenza a tutte le modifiche che si vogliono fare. Ad esempio l'azione di una forza non è sempre uguale, dipende, come sappiamo, dalla massa del corpo, e la connessione tra forza e massa è esplicitata nel secondo principio della dinamica.

Analogamente, anche nella rotazione di un corpo l'effetto non sempre è lo stesso: in questo caso la resistenza che il corpo oppone è data da una nuova grandezza, il Momento d'Inerzia.

Cos'è il momento di inerzia? come abbiamo anticipato, non è un vero e proprio momento, in quanto non si definisce tramite un prodotto vettoriale; infatti è una grandezza scalare, legata alla massa di un corpo e alla distanza che il corpo ha dal centro di rotazione. Partiamo dal caso più semplice:

Il momento di inerzia si misura in chilogrammi per metri al quadrato (kg·m²). Osserviamo che il momento di inerzia è sempre positivo, ed è direttamente proporzionale alla massa del punto e al quadrato della sua distanza dal centro; se un punto si trova sul centro di rotazione, il suo momento d'inerzia è zero.

In un sistema composto di vari punti, ognuno con la propria massa e la propria distanza, il momento d'inerzia totale è ottenuto dalla somma aritmetica dei momenti di inerzia dei singoli punti materiali che lo costituiscono. Normalmente le masse e le distanze non sono tutte uguali, il ché rende un po' complesso calcolare il momento di inerzia totale.

^
Torna su

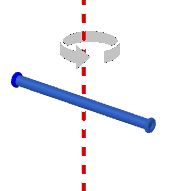
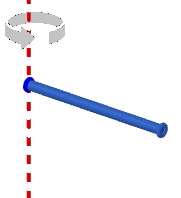
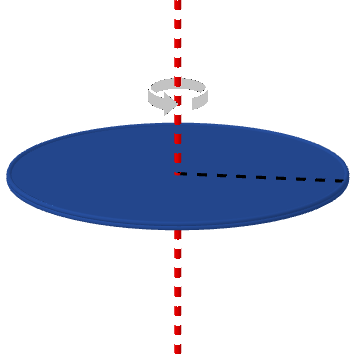
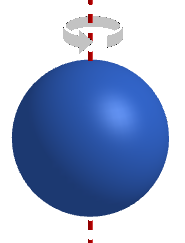
Momento d'inerzia dei corpi rigidi

Come possiamo calcolare il momento di inerzia di un corpo rigido, dal momento che lui ha infiniti punti? Il calcolo non è semplice, in quanto non si può fare tramite una semplice addizione. Inoltre il momento di inerzia di uno stesso oggetto varia anche a seconda dell'asse di rotazione considerato: se intorno ad uno dei suoi assi di simmetria, o ad un'altra retta, o ad un vincolo esterno…
Nel caso le masse e le distanze siano tutte uniformi (come ad esempio una sfera vuota, che gira intorno a se stessa) allora possiamo aiutarci con le proprietà geometriche (in questo caso usiamo la formula della superficie sferica). In casi più complessi, dobbiamo ricorrere a strumenti più potenti, come gli integrali.

Ecco di seguito i momenti d'inerzia di alcune forme particolari, in cui consideriamo, per semplicità, che la massa sia distribuita uniformemente su tutto il volume; nelle figure seguenti l'asse di rotazione è tratteggiato in rosso, mentre i raggi sono tratteggiati in nero.

Momenti di inerzia di oggetti con forme particolari

♦ Asta sottile 1 ♦ Asta rettilinea di massa m e lunghezza ℓ; spessore e larghezza trascurabili. Asse di rotazione: asse di simmetria perpendicolare alla lunghezza. ℐ = m ℓ ² ⁄ 12

♦ Asta sottile 2 ♦ Asta rettilinea di massa m e lunghezza ℓ; spessore e larghezza trascurabili. Asse di rotazione: asse perpendicolare alla lunghezza passante per un suo estremo. ℐ = m ℓ ² ⁄ 3

♦ Anello sottile 1 ♦ Anello circolare di massa m e raggio esterno R; raggio interno trascurabile. Asse di rotazione: asse di simmetria perpendicolare al piano dell'anello. ℐ = m R²

♦ Anello sottile 2 ♦ Anello circolare di massa m e raggio esterno R; raggio interno trascurabile. Asse di rotazione: asse di simmetria complanare all'anello. ℐ = m R² ⁄ 2

♦ Disco sottile 1 ♦ Disco circolare di massa m e raggio R; spessore trascurabile. Asse di rotazione: asse di simmetria perpendicolare al piano del disco. ℐ = m R² ⁄ 2

♦ Disco sottile 2 ♦ Disco circolare di massa m e raggio R; spessore trascurabile. Asse di rotazione: asse di simmetria complanare al disco. ℐ = m R² ⁄ 4

♦ Cilindro vuoto 1 ♦ Superficie cilindrica vuota, di massa m, raggio di base R e altezza h. Asse di rotazione: asse di simmetria centrale (passante per le basi). ℐ = m R² Osserviamo che in questa situazione l'altezza non influenza il momento d'inerzia.

♦ Cilindro vuoto 2 ♦ Superficie cilindrica vuota, di massa m, raggio di base R e altezza h. Asse di rotazione: asse di simmetria trasversale (passante per la superficie laterale). ℐ = m (6R² + h²) ⁄ 12

♦ Cilindro pieno 1 ♦ Cilindro solido pieno, di massa m, raggio di base R e altezza h. Asse di rotazione: asse di simmetria centrale (passante per le basi). ℐ = m R² ⁄ 2 Osserviamo che in questa situazione l'altezza non influenza il momento d'inerzia.

♦ Cilindro pieno 2 ♦ Cilindro solido pieno, di massa m, raggio di base R e altezza h. Asse di rotazione: asse di simmetria trasversale (passante per la superficie laterale). ℐ = m (3R² + h²) ⁄ 12

♦ Sfera vuota ♦ Superficie sferica vuota, di massa m e raggio R. Asse di rotazione: un suo qualunque asse di simmetria. ℐ = m R² · 2 ⁄ 3

♦ Sfera piena ♦ Sfera solida piena, di massa m e raggio R. Asse di rotazione: un suo qualunque asse di simmetria. ℐ = m R² · 2 ⁄ 5

^
Torna su

Inerzia e rotazione

Consideriamo un punto materiale che ruoti di moto circolare di raggio R; osserviamo che, usando la definizione, possiamo scomporre il modulo del momento angolare come prodotto tra il braccio e la quantità di moto:

L = b · p = b · m · v

La velocità corrisponde alla velocità tangenziale di rotazione, quindi: v = ω · R, dove R, il raggio di rotazione, coincide con il braccio. Quindi:

L = b · m · v = b · m · ω · b

L = b² · m · ω

La quantità b²·m è il momento di inerzia ℐ del corpo, come abbiamo visto in precedenza. Possiamo allora scrivere il modulo del momento angolare anche in una nuova forma:

Nel caso di sistemi formati da più punti materialli, il modulo del momento angolare si può ottenere calcolando la somma dei singoli momenti di inerzia e poi moltiplicare il risultato per la velocità angolare, uguale per tutti i punti.

Questo risultato si estende anche ai corpo rigidi: il momento angolare di un corpo di qualunque forma e dimensione si può calcolare come prodotto tra suo momento di inerzia (che ad esempio può esser calcolato con le formule viste sopra) e la sua velocità angolare.

^
Torna su

<<< Precedente   -   Successivo >>>