|
★ ★ ☆
<<< Precedente -
Successivo >>>
CONTENUTO DELLA PAGINA
Studio del segno
Studiare la disequazione ƒ(x) > 0
Rappresentazione grafica
Studio del segno
Il segno di una funzione è il segno dell'immagine y = ƒ(x) di un valore x, ossia il fatto che l'immagine sia positiva o negativa.
|
Esempio 11. Studiamo il segno dei punti della funzione analizzata nell'esempio 1:
ƒ(x) = x² − 9
Svolgimento. Di questa funzione abbiamo calcolato le immagini di alcuni valori di x; in base alla tabella costruita nel precedente esempio possiamo osservare che:
- se x = −4, 0, 5, allora l'immagine (e quindi la funzione) è positiva;
- se x = −1, ½, 2, allora l'immagine (e quindi la funzione) è negativa;
- se x = 3 allora l'immagine è zero, quindi abbiamo un punto d'intersezione con l'asse x.
|
Se la funzione ha segno positivo (ƒ(x) > 0) allora il punto del grafico corrispondente si trova nel I o nel II quadrante, quindi sopra l'asse x.
Se al contrario la funzione ha segno negativo (ƒ(x) < 0) allora il punto del grafico corrispondente si trova nel III o nel IV quadrante, quindi sotto l'asse x.
Lo studio del segno consiste del determinare per quali valori di x, le immagini siano sopra l'asse delle x e per quali x siano sotto; lo svolgimento dello studio del segno consiste in due passi:
- studiare la disequazione ƒ(x) > 0 e sintetizzare il risultato utilizzando la tabella per lo studio del segno (vedi le regole sulle disequazioni);
- rappresentare i risultati ottenuti all'interno del piano cartesiano, cancellando le parti di piano (sopra o sotto l'asse x) non interessate dalla funzione.
Vediamo ora in dettaglio questi due passi.
^
Torna su
1° passo: studiare la disequazione ƒ(x) > 0
Lo studio di una disequazione dipende molto dal tipo di funzione; generalmente la funzione da studiare è un polinomio o una frazione, per cui è sufficiente scomporre in fattori e studiarli singolarmente, mettendo insieme i risultati in una tabella dei segni.
Nel caso particolare di disequazioni di I grado intere il risultato si può ottenere in pochi passaggi; nel caso di disequazioni di II grado intere possiamo ricorrere allo studio della parabola associata.
|
Esempio 12 – 1ª parte. Studiamo il segno della funzione:
ƒ(x) = x³ − 4x
Svolgimento. Il Dominio di tale funzione è tutto l'insieme ℝ, per cui possiamo studiare direttamente la disequazione:
x³ − 4x > 0
Essendo un polinomio di III grado, proviamo a scomporre in fattori; raccogliamo x a fattor comune, quindi applichiamo la somma per differenza:
x (x² − 4) > 0
x (x − 2) (x + 2) > 0
Abbiamo ottenuto 3 fattori distinti, da studiare separatamente:
F1. x > 0
F2. x − 2 > 0 ⇒ x > 2
F3. x + 2 > 0 ⇒ x > −2
Inseriamo i risultati parziali nella tabella per lo studio dei segni:
| x : |
|
−2 |
|
0 |
|
+2 |
|
| F1 |
− |
− |
− |
0 |
+ |
+ |
+ |
| F2 |
− |
− |
− |
− |
− |
0 |
+ |
| F3 |
− |
0 |
+ |
+ |
+ |
+ |
+ |
| ƒ(x) |
− |
0 |
+ |
0 |
− |
0 |
+ |
Conclusione: la funzione assume i seguenti segni:
- positiva (ƒ(x) > 0) ⇔ −2 < x < 0 ∨ x > 2;
- negativa (ƒ(x) < 0) ⇔ x < −2 ∨ 0 < x < 2.
|
|
Esempio 13. Studiamo il segno della funzione:
| y = |
10 − 2x
log3 (x² − 4x + 3) − 1 |
Svolgimento. Il Dominio di tale funzione deve rispettare le seguenti c.e.:
- per il logaritmo: x² − 4x + 3 > 0
- per la frazione: log3 (x² − 4x + 3) − 1 ≠ 0
La prima si risolve studiando la parabola associata, ottenendo: x ≤ 1 ∨ x ≥ 3.
La seconda si risolve studiando l'equazione logaritmica associata, ottenendo: x = 0 ∨ x = 4.
D = { ∀x∈ ℝ : (x ≤ 1 ∨ x ≥ 3) ∧ x ≠ 0 ∧ x ≠ 4 }
Facendo attenzione a tali condizioni, passiamo allo studio del segno della funzione, risolvendo la disequazione:
| 10 − 2x
log3 (x² − 4x + 3) − 1 |
> 0 |
Essendo una frazione, possiamo studiare separatamente numeratore e denominatore:
n. 10 − 2x > 0 ⇒ x < 5
d. log3 (x² − 4x + 3) − 1 > 0
Il denominatore contiene un logaritmo, per cui dobbiamo studiare la disequazione logaritmica: applicando le proprietà dei logaritmi, tale disequazione si trasforma in:
log3 (x² − 4x + 3) > 1
x² − 4x + 3 > 3
x² − 4x > 0
Tale disequazione ci porta da altri due fattori:
d1. x > 0
d2. x > 4
Inseriamo i risultati parziali nella tabella per lo studio dei segni:
| x : |
|
0 |
|
4 |
|
5 |
|
| n |
+ |
+ |
+ |
+ |
+ |
0 |
− |
| d1 |
− |
0 |
+ |
+ |
+ |
+ |
+ |
| d2 |
− |
− |
− |
0 |
+ |
+ |
+ |
| ƒ(x) |
+ |
0 |
− |
0 |
+ |
0 |
− |
Controllando il Dominio, osserviamo che la funzione non è definita per 1 < x < 3.
Conclusione: la funzione:
- non esiste ⇔ 1 < x < 3 ∨ x = 0 ∨ x = 4;
- è positiva (ƒ(x) > 0) ⇔ x < 0 ∨ 4 < x < 5;
- è negativa (ƒ(x) < 0) ⇔ 0 < x < 1 ∨ 3 < x < 4 ∨ x > 5;
|
^
Torna su
2° passo: rappresentazione grafica
Possiamo trasferire i risultati ottenuti dalla tabella per lo studio del segno nel piano cartesiano: riportiamo i riferimenti sull'asse x, rispettando i vincolidel Dominio: linee verticali intere o tratteggiate, a seconda di come compaiono nel Dominio; ogni valore x che non compare esplicitamente nel Dominio (ma rispetta comunque le condizioni) avrà una riga verticale tratteggiata.
Abbiamo quindi diviso il piano cartesiano in fasce verticali; ad ogni fascia corrisponde un segno, secondo il risultato della tabella al passo precedente:
- se ad una fascia corrisponde un risultato positivo (+) allora la funzione si troverà sopra l'asse delle x, e di conseguenza dobbiamo cancellare la zona inferiore;
- se ad una fascia corrisponde un risultato negativo (−) allora la funzione si troverà sotto l'asse delle x, e di conseguenza dobbiamo cancellare la zona superiore.
|
Esempio 12 – 2ª parte. Rappresentiamo nel piano cartesiano il segno della funzione ƒ(x) = x³ − 4x studiata prima.
Svolgimento. Dobbiamo disegnare 3 righe verticali, in corrispondenza dei valori x 0 −2, x = 0, x = 2; essendo il Dominio tutto l'insieme ℝ, ogni riga verticale è tratteggiata.
A questo punto vediamo cosa segnare nel piano:
- nella fascia più a sinistra, per x < −2, la funzione è negativa, quindi si trova sotto l'asse x: cancelliamo la zona superiore;
- nella seconda fascia, per −2 < x < 0, la funzione è positiva, quindi si trova sopra l'asse x: cancelliamo la zona inferiore;
- nella terza fascia, per 0 < x < 2, la funzione è negativa, quindi si trova sotto l'asse x: cancelliamo la zona superiore;
- nell'ultima fascia, per x > 2, la funzione è positiva, quindi si trova sopra l'asse x: cancelliamo la zona inferiore.
Conclusione: ecco il risultato che si ottiene (in grigio le zone cancellate):
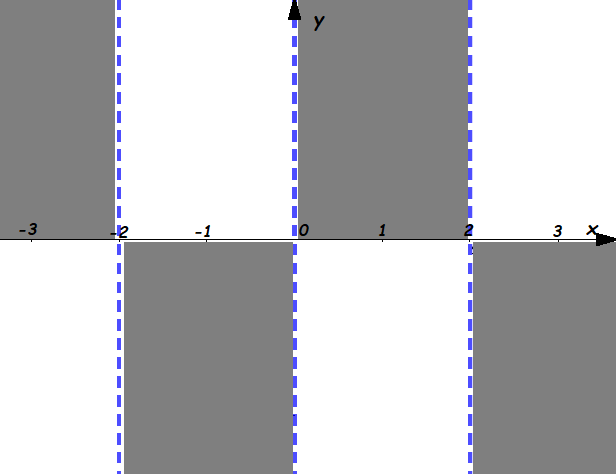
Figura 1
|
^
Torna su
<<< Precedente -
Successivo >>>
|
