Equazione canonica - Proprietà principali - Altre proprietà

★ ★ ☆

<<< Precedente   -   Successivo >>>

CONTENUTO DELLA PAGINA
Definizione
Casi particolari
Equazione generale

Definizione

Nel piano cartesiano studiamo parabole aventi la direttrice parallela agli assi, quindi di equazione x = j oppure y = k

Primo caso: direttrice y = k (parallela all'asse x). La parabola si rappresenta per mezzo di un'equazione del tipo:

con a, b, c coefficienti reali.

Secondo caso: direttrice x = j (parallela all'asse y). La parabola si rappresenta con un'equazione del tipo:

In queste pagine, per semplicità, vengono trattate solo parabole del primo tipo.
L'insieme dei punti di una parabola è dato dall'insieme di tutti e soli i punti P di coordinate (x₀, y₀) che verificano l'equazione della parabola:

y₀ = ax₀² + bx₀ + c

La parabola possiede un asse di simmetria, ortogonale alla direttrice; il punto d'intersezione tra la parabola e l'asse è chiamato vertice della parabola.

^
Torna su

Casi particolari

• Se a = 0 la parabola degenera in una retta di equazione y = bx + c; se vogliamo studiare parabole non degeneri è quindi necessario imporre la condizione a ≠ 0.

  

• Se b = 0 la parabola ha equazione y = ax² + c, ed è simmetrica rispetto all'asse y: infatti se consideriamo punti sulla parabola aventi ascissa opposta, l'ordinata ha lo stesso valore.
• Se c = 0 la parabola ha equazione y = ax² + bx, e passa per l'origine.

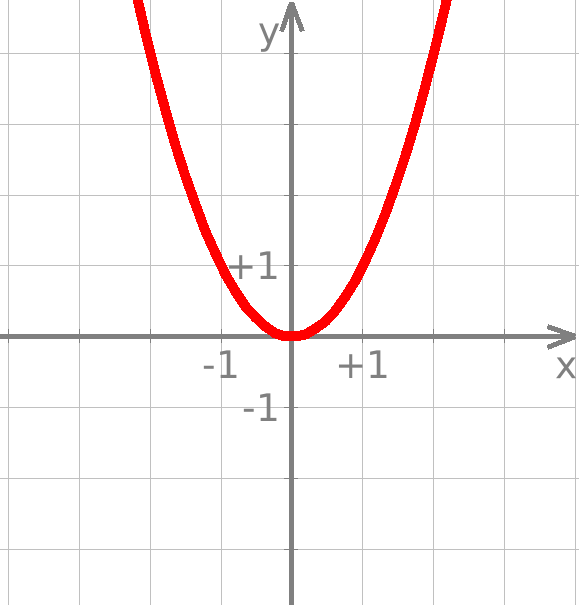
In particolare se b = c = 0 e a = 1 otteniamo l'equazione più semplice possibile di una parabola: l'equazione diventa y = x², una parabola passante per l'origine e simmetrica rispetto all'asse y; il grafico di questa parabola (vedi figura 1) è utilizzato per rappresentare una proporzionalità quadratica tra due grandezze (limitando il grafico al primo quadrante), ad esempio il lato e l'area di un quadrato.

^
Torna su

Equazione generale

Fissiamo un punto F(α, β) e una retta d: y = k, con k ≠ β; vogliamo ricavare l'equazione di una parabola avente il punto F come fuoco e la retta d come direttrice, imponendo la condizione del luogo.

Sia P(x, y) un punto qualunque del piano; vogliamo che la distanza di P da F sia uguale alla distanza di P da d (vedi figura 2).

La distanza di P da F è la lunghezza del segmento PF, e vale:

PF = √(x − α)² + (y − β)²

e la distanza di P da d è la lunghezza del segmento PH, dove H è la proiezione di P su d, e vale:

PH = | y − k |

uguagliando le due espressioni si ottiene:

| y − k | = √(x − α)² + (y − β)²

eleviamo al quadrato:

y² − 2ky + k² = x² − 2αx + α² + y² − 2βy + β²;

e svolgendo i calcoli, isolando la y:

2βy − 2ky = x² − 2αx + α² + β² − k² ;

(2β − 2k)y = x² + (− 2α)x + (α² + β² − k²) ;

essendo k ≠ β possiamo dividere ambo i membri per (2β − 2k), e porre:

• a = 1 / (2β − 2k)
• b = (− 2α) / (2β − 2k)
• c = (α² + β² − k²) / (2β − 2k)

ottenendo l'equazione generale:

^
Torna su

<<< Precedente   -   Successivo >>>