Introduzione - Definizioni - Operazioni - Forme indet. - Continuità - Asintoti

★ ★ ☆

<<< Precedente   -   Successivo >>>

CONTENUTO DELLA PAGINA
Asintoti verticali
Asintoti orizzontali
Asintoti obliqui

Un asintoto è una retta molto particolare del piano cartesiano, che possiamo utilizzare come guida per la nostra funzione; infatti una retta fa da asintoto per una funzione, se tale funzione graficamente si avvicina sempre più alla retta, senza mai arrivare a toccarla. Da un punto di vista topologico, si può dire che una funzione e un asintoto sono tangenti all'infinito.

Ci sono molte funzioni che possiedono asintoti, il che ci aiuta non poco per la rappresentazione grafica di una funzione: gli asintoti forniscono lo scheletro di una funzione, ci dicono le direzioni che la funzione deve prendere. Un esempio tipico di funzione che possiede asintoti è l'iperbole, che si studia in geometria analitica.

Osservazione: partiamo con il dire una cosa importante: ogni asintoto dipende da un limite; quindi per studiare un asintoto dobbiamo decidere a cosa volgiamo far tendere la x; il fatto che una retta sia un asintoto non è una proprietà generale, ma locale, proprio perché dipende dal limite che stiamo studiando: una retta può esser asintoto per una zona (un ramo) della funzione, ma non esserlo per un'altra zona (un altro ramo); questo comporta che in alcuni casi la funzione possa toccare, o intersecare la retta che fa da asintoto, o allontanarsi da essa.

Asintoti verticali

Un asintoto verticale è una retta di equazione x = x₀, dove x₀ è un punto di discontinuità asintotica; questo vuol dire che:

Il limite per x → xₒ può valere solo da destra, solo da sinistra o da entrambe le parti.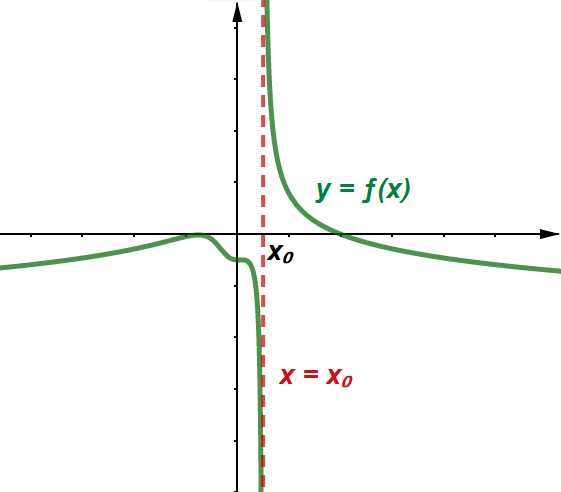

Un asintoto verticale interrompe sempre la funzione: è un muro che non può esser attraversato dalla funzione; come si vede nella figura 4, la funzione tende a seguire la retta, quindi anche il grafico della funzione si inclina in verticale sempre di più fino a sembrare parallelo alla retta. In questa figura possiamo osservare che quando x → xₒ⁻ (da sinistra) allora la funzione tende a −∞, mentre quando x → xₒ⁺ (da destra) allora la funzione tende a +∞; ovviamente questo è un caso, possono capitare combinazioni diverse.

In alcune situazioni particolari, come abbiamo spiegato, la funzione può anche arrivare a toccare l'asintoto, purchè in una zona diversa da quella studiata nel limite.

^
Torna su

Asintoti orizzontali

Un asintoto orizzontale è una retta di equazione y = L, essendo L il limite finito della funzione, quando x diverge a ± ∞; questo vuol dire che, affinch´ la funzione possieda un asintoto orizzontale, deve accadere che:

Anche in questo caso il limite può valere solo per x → +∞ o solo per x → −∞, e di conseguenza il comportamento della funzione nelle altre zone sono è vincolato all'asintoto.

Un asintoto orizzontale non interrompe la funzione: è una guida a cui la funzione tende a stabilizzarsi, man mano che si allontana dall'origine; come si vede nell'esempio di figura 5, la funzione tende a seguire la retta solo a destra, quindi per x → +∞, e di conseguenza il grafico della funzione verso destra diventa quasi orizzontale, fino a sembrare parallelo alla retta; possiamo osservare anche che al centro la curva effettivamente tocca la retta, e a sinistra invece si allontana sempre di più da essa; questo vuol dire che l'asintoto vale sono per la parte destra del grafico.

^
Torna su

Asintoti obliqui

Un asintoto obliquo è una retta di equazione y = mx + q, con m ≠ 0; si ha un asintoto obliquo quando la funzione diverge, per x che tende a ± ∞;, con una crescita lineare; affinch´ la retta sia effettivamente un asintoto obliquo, è necessario che siano verificate alcune condizioni; la prima è:

Dove anche in questo caso il limite può valere solo per x → +∞ o solo per x → −∞, e di conseguenza il comportamento della funzione nelle altre zone sono è vincolato all'asintoto.

Un asintoto obliquo, come quello orizzontale, non interrompe la funzione: è una guida a cui la funzione tende a stabilizzarsi, man mano che si allontana dall'origine; come si vede nell'esempio di figura 6, la funzione tende a seguire la retta solo a destra, quindi per x → +∞, e di conseguenza il grafico della funzione verso destra si allinea, fino a sembrare parallelo alla retta; possiamo osservare anche che vicno al centro la curva effettivamente incrocia un paio di volte la retta, e a sinistra invece si allontana sempre di più da essa; questo vuol dire che l'asintoto vale sono per la parte destra del grafico.

La presenza di un asintoto obliquo per un determinato limite esclude la presenza di un asintoto orizzontale in quello stesso limite: per il teorema di unicità del limite, se la funzione diverge ad infinito, non può convergere ad un valore L.

Tuttavia il verificare che la funzione diverga ad infinito, non ci garantisce che si abbia un asintoto obliquo; per esser certi dobbiamo verificare altri due limiti.
Per prima cosa dobbiamo controllare che la funzione abbia un andamento lineare, ossia che cresca in modo simile ad x:

Dove il valore m, che non deve venire nullo, sarà il coefficiente angolare della retta.
Poi dobbiamo determinare la quota q di tale retta, mediante l'ultimo limite:

Ovviamente entrambi i limiti devono esistere ed esser finiti.

^
Torna su

<<< Precedente   -   Successivo >>>