|
★ ★ ☆
<<< Precedente -
Successivo >>>
CONTENUTO DELLA PAGINA
I numeri reali
Radici e radicali
Regole dei radicali
Forma esponenziale dei radicali
I numeri reali
Simbolo: ℝ
Cardinalità: ℵ1. L'insieme dei numeri reali non può esser messo in corrispondenza biunivoca con gli insiemi precedenti.
Definizione: La definizione di questo insieme non è molto semplice: l'insieme dei numeri reali comprende tutti i numeri usati normalmente in matematica: i numeri interi, decimali limitati, decimali periodici (ossia i razionali) e aperiodici; un numero reale è un qualunque numero con una qualunque successione di cifre decimali, sia periodiche sia casuale… anche se non è molto rigosa, tuttavia tale definizione esprime bene l'idea.
Formalmente sono definiti introducendo i "limiti" finiti di tutte le succesioni di numeri razionali.
L'insieme dei numeri reali contiene:
- i numeri
algebrici , i numeri che si possono ottenere come zeri di un polinomio a coefficienti interi; ne fanno parte tutti i razionali e i radicali (es. √2, il rapporto aureo);
- i numeri
trascendenti , tutti i numeri reali che non sono algebrici (es. pi greco, il numero di Nepero)
L'insieme dei numeri reali è molto vasto e i razionali, gli interi e i naturali, non sono che una piccola parte dei numeri reali!
Di seguito è riportata un'illustrazione schematica dei vari sottoinsiemi di cui è composto l'insieme dei numeri reali.
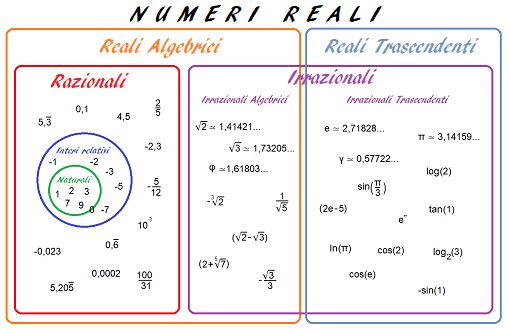 Figura 1
Figura 1
Operazioni: l'addizione, la sottrazione, la moltiplicazione, la potenza e la radice con indice dispari all'interno dei numeri reali sono ben definite, si possono sempre fare e il risultato che si ottiene è sempre un numero reale.
Al contrario le altre operazioni non sono ben definite, si possono fare con le stesse limitazioni che si hanno con i numeri razionali:
- la divisione si può fare solo se il divisore è diverso da zero;
- la radice con indice pari si può fare solo se il radicando è positivo ed è una potenza di esponente multiplo dell'indice della radice;
- il logaritmo si può fare solo se l'argomento è positivo.
Osservazione: dal punto di vista pratico, svolgere operazioni tra numeri reali spesso è impossibile, non perché il risultato non esista, ma perché non possiamo calcolarlo in modo preciso: già il solo scrivere per esteso un numero reale non sempre è possibile!
Per operare tra numeri reali, possiamo usare le proprietà delle varie operazioni coinvolte, possiamo lasciare il numero in formato simbolico (come pi greco), oppure possiamo approssimare i numeri a numeri razionali.
Proprietà: dalla definizione segue che l'insieme dei numeri reali può esser associato all'insieme di tutti i sottoinsiemi di numeri naturali: formalmente si scrive che ℝ ≅ 2ℕ, ossia ℝ può esser messo in corrispondenza biunivoca con l'insieme delle parti di ℕ; questo comporta che l'insieme ℝ è un insieme infinito, denso e non numerabile: a differenza degli insiemi precedenti, è un insieme continuo e c'è una corrispondenza biunivoca tra i numeri reali e i punti di una retta; come conseguenza si ha che l'insieme dei nueri reali è un insieme completo.
Riassumendo:
- ℕ - infinito, ordinato, discreto, numerabile;
- ℤ - infinito, ordinato, discreto, numerabile;
- ℚ - infinito, ordinato, denso, numerabile;
- ℝ - infinito, ordinato, denso, continuo, completo;
Dal punto di vista dell'algebra lineare, la terna ( ℝ, +, × ) forma un campo.
^
Torna su
Radici e radicali
Con il termine radicale si intende l'espressione formata dal simbolo di radice, dall'indice di radice (il numero piccolino in alto prima della radice) e dal radicando (l'espressione dentro la radice).
L'operazione di estrazione a radice, o semplicemente di radice, è una delle due operazioni inverse dell'elevamento a potenza (l'altra è il logaritmo): come abbiamo visto, la radice di un numero reale, se esiste, è quel numero reale che elevato a potenza mi fa riottenere il numero dato:
Nel caso in cui l'indice n non sia esplicitamente scritto, è sottointeso che valga 2; il caso invece sia 1 non viene considerato in quanto è banale: il risultato della radice coincide con il radicando.
Al contrario il radicando deve esser sempre scritto, non è mai sottointeso.
Un radicale può essere:
radicale numerico , se nell'indice e nel radicando compaiono solo numeri;
radicale algebrico , se nell'indice e nel radicando compaiono anche espressioni letterali.
Affinché la radice esista, è necessario fare attenzione al valore dell'indice e del radicando presenti; nel caso in cui ci limitiamo a considerare solo indici interi non nulli, allora se l'indice della radice è un numero pari, il radicando non può essere un numero negativo.
Più in generale, dal momento che se consideriamo un radicale algebrico l'indice e il radicando possono essere numeri reali qualunque, dobbiamo porre importanti condizioni di esistenza:
In generale quindi la condizione per il radicando si applica per qualunque indice, non solo per quelli pari; ovviamente se l'indice è un numero intero dispari, allora la condizione sul radicando non è più necessaria.
Osservazione: lo svolgimento di un'operazione di radice non sempre (o meglio, quasi mai) ci porta a risultati numerici interi, o anche razionali: nel 99% dei casi il risultato di una radice è un numero irrazionale, quindi non può esser conosciuto completamente; per questo in algebra se una radice è irrazionale non la si risolve per niente, considerandola come una qualunque espressione letterale che non si conosce.
È importante saper gestire i radicali all'interno di espressioni algebriche, anche quando non si possono risolvere, e il modo migliore di gestire un radicale è quello di vederlo come una lettera, o come la parte letterale di un monomio, in quanto di fatto non sappiamo il suo valore reale.
Un radicale può avere anche un coefficiente numerico davanti e tale coefficiente numerico è legato al radicale da una moltiplicazione (sottointesa). Se il radicale non possiede un coefficiente numerico esplicito, è sottinteso sia 1; se invece il coefficiente è zero, allora si scrive solo zero, il radicale non si scrive.
1 ⁵√2 ≡ ⁵√2
0 ⁵√2 ≡ 0
|
Due radicali sono simili se hanno stesso indice e stesso radicando.
|
Quindi due radicali simili possono avere diversi solo gli eventuali coefficienti davanti, proprio come i monomi:
5 ³√12, ³√12, − 3 ³√12, 2 ³√12
^
Torna su
Regole dei radicali
In queste formule supponiamo sempre che siano rispettate le condizioni di esistenza per i radicali: indice diverso da zero e radicando non negativo.
♦ Proprietà, fondamentale ♦
La prima proprietà, fondamentale, viene dalla definizione:
|
Un radicale avente come radicando una potenza con esponente uguale all'indice della radice, equivale alla base della potenza:
|
Infatti, essendo potenze e radici due operazioni opposte, si annullano a vicenda.
Questa proprietà è un caso particolare di una regola più generale che è la proprietà invariantiva dei radicali.
|
Proprietà invariantiva
Moltiplicando (o dividendo) l'indice di un radicale e l'esponente del radicando per uno stesso numero p ≠ 0, si ottiene un radicale equivalente a quello iniziale.
|
|
Esempio 10. Vediamo alcuni radicali equivalenti
Possiamo aumentare gli indici con delle moltiplicazioni:
³√ 4 →
³ ²√ 4 ² →
⁶√ 16
Possiamo diminuire gli indici con delle divisioni (se possibile):
32√ 5 2 →
32 ∶ 2√ 5 2 ∶ 2 →
16√ 5
²¹√ 8 →
²¹√ 2 ³ →
⁷√ 2
|
♦ Operazioni ♦
Le operazioni tra radicali riprendono le proprietà delle potenze, oltre a sfruttare, come abbiamo detto, anche le regole dei monomi. Restando nel rispetto delle condizioni di esistenza, abbiamo:
- Addizione e sottrazioni: queste operazioni possono esser svolte solo se i radicali sono simili, altrimenti l'espressione rimane così com'è.
La somma (o differenza) tra due radicali simile è un radicale anch'esso simile, avente come coefficiente numerico la somma (o differenza) dei coefficienti dei due radicali iniziali.
|
Esempio 11. Ecco alcune piccole espressioni con addizioni e sottrazioni tra radicali.
Con radicali simili.
3 ³√ 4 − 5 ³√ 4 + 4 ³√ 4 =
= (3 − 5 + 4) ³√ 4 = 2 ³√ 4
Con gruppi di radicali simili.
7 √ 5 + √ 3 − 3 √ 5 + 4 √ 3 =
= (5 − 3) √ 5 + (1 + 4) √ 3 =
= 2 √ 5 + 5 √ 3
Con radicali che possono diventare simili.
3 ⁶√ 8 + 2 ¹²√ 64 =
3 ⁶√ 2 ³ + 2 ¹²√ 2 ⁶ =
3 √ 2 + 2 √ 2 =
= (3 + 2) √ 2 = 5 √ 2
|
- Moltiplicazione: la moltiplicazione tra due radicali si può fare solo se i radicali hanno lo stesso indice: in tal caso il prodotto che si ottiene è un radicale anch'esso con lo stesso indice e avente per coefficiente il prodotto dei coefficienti, e per radicando il prodotto tra i radicandi:
Nel caso in cui gli indici siano differenti occorre aggiustare i radicali con la proprietà invariantiva, cercando di ottenere gli stessi indici (in genere basta calcolare il m.c.m. tra gli indici).
- Divisione: anche la divisione tra due radicali si può fare solo se i radicali hanno lo stesso indice: in tal caso il quoziente che si ottiene è un radicale anch'esso con lo stesso indice e avente per coefficiente il quoziente dei coefficienti, e per radicando il quoziente tra i radicandi:
Nel caso in cui gli indici siano differenti occorre aggiustare i radicali, calcolando il m.c.m. tra gli indici.
|
Esempio 12. Ecco alcune piccole espressioni con moltiplicazioni e divisioni tra radicali.
Con radicali aventi stesso indice.
(2 ⁶√ 5 ) · (6 ⁶√ 10 ) ∶ (4 ⁶√ 2 ) =
= (2 · 6 ∶ 4) ⁶√ 5 · 10 ∶ 2 =
= 3 ⁶√ 25 = 3 ³√ 5
Con radicali aventi indici differenti.
2 √ 3 · ³√ 4 · ⁶√ 2 =
= 2 ⁶√ 3 ³ · ⁶√ 4 ² · ⁶√ 2 =
= 2 ⁶√ 3 ³ · 4 ² · 2 =
= 2 ⁶√ 9 · 16 · 2 = 2 ⁶√ 288
|
- Elevamento a potenza la potenza di un radicale è un radicale avente per indice lo stesso indice e per radicando la potenza del radicando inziale (ovviamente è possibile che esponente e indice si semplifichino grazie alla proprietà invariantiva).
- Estrazione di radice la radice di un radicale è un radicale avente per indice il prodotto degli indici delle radici e per radicando lo stesso radicando inziale.
- Logaritmo il logaritmo di un radicale è una frazione avente a numeratore il logaritmo del radicando e a denominatore l'indice del radicale.
♦ Trasporto di un fattore dentro o fuori il segno di radice ♦
Abbiamo visto che la moltiplicazione e la divisione possono unire due radicali, e li possono anche separare, purché in entrambi i casi sia conservato lo stesso indice di radice:
Ciò risulta particolarmente utile quando uno dei due fattori non è un radicale, ma un numero normale; ricordiamo che, applicando la proprietà fondamentale, ogni numero non negativo può esser scritto come radicale:
Quindi un fattore fuori dal segno di radice, può esser inserito all'interno di una radice, acquistando un esponente uguale all'indice della radice; tale operazione si chiama trasporto dentro il segno di radice:
Tale regola si può applicare solo in presenza di fattori, quindi di moltiplicazioni, o al massimo di divisioni. Quindi ad esempio:
2 · ⁴√ 5 =
⁴√ 2⁴ · 5 =
⁴√ 80
Analogamente possiamo fare anche il contrario: se all'interno di un radicale compare un fattore avente un esponente uguale (o multiplo) dell'indice di radice, si possono separare le radice in modo da poter semplificare il fattore considerato, applicando la proprietà invariantiva. Questa operazione si chiama trasporto fuori dal segno di radice:
Anche in questo caso questa regola si può applicare solo in presenza di fattori, quindi di moltiplicazioni, o al massimo di divisioni; ovviamente per applicare il trasporto fuori dal segno di radice, il primo passo è scomporre il radicando in fattori primi, per riconoscere eventuali potenze semplificabili. Quindi ad esempio:
√ 72 = √ 2³ · 3² =
= √ 2² · √ 2 · √ 3² =
= 2 · √ 2 · 3 = 6 √ 2
♦ Razionalizzazione ♦
La razionalizzazione è un processo con il quale modifichiamo un'espressione irrazionale (senza cambiarne il risultato) in modo tale che una sua parte diventi razionale, ossia senza radicali.
Ovviamente un'espressione irrazionale, quindi con radicali che non si possono semplificare del tutto, non potrà mai diventare completamente razionale, perché altrimenti si cambierebbe il risultato; tuttavia possiamo rimescolare la nostra espressione per far s&iagrave; che una sua parte non abbia più radicali.
In particolare, se abbiamo una frazione avente radici al denominatore, vogliamo scrivere una frazione equivalente, applicando le proprietà dei radicali e delle frazioni, in modo tale che il denominatore non abbia più radici (a costo eventualmente di complicare il numeratore).
Questa tecnica si chiama "razionalizzazione del denominatore", e sfrutta la proprietà invariantiva delle frazioni: moltiplicando o dividendo numeratore e denominatore di una frazione per uno stesso numero non nullo, otteniamo una frazione equivalente a quella iniziale.
Ma per cosa dobbiamo moltiplicare? dipende da quali radicali sono presenti al denominatore, in quanto vogliamo moltiplicare per qualcosa che renda il radicale semplificabile.
Vediamo i due casi più semplici.
- Se il denominatore possiede un solo radicale e nient'altro, occore moltiplicare per un radicale avente lo stesso indice, e radicando "complementare", ossia tale da rendere il prodotto semplificabile.
L'obiettivo è far sì che il radicando prodotto abbia esponenti multipli dell'indice di radice, e quindi tutto il radicale si possa semplificare.
- Se ad esempio al denominatore ho √5, moltiplico sopra e sotto per √5, perché così sotto ottengo √25 che si può risolvere.
- Se al denominatore ho ³√2, moltiplico sopra e sotto per ³√4, perché così sotto ottengo ³√8 che si può risolvere.
- Se al denominatore ho ⁶√3⁵, moltiplico sopra e sotto per ⁶√3, perché così sotto ottengo ⁶√3⁶ che si può risolvere.
E così via…
- Se il denominatore possiede due termini, di cui uno è un radicale con indice 2 e l'altro è un numero razionale, oppure se entrambi sono radicali con indice 2, possiamo sfruttare il prodotto notevole somma per differenza, e moltiplicare sopra e sotto per l'operazione opposta a quella presente nel denominatore.
- Se ad esempio al denominatore ho √3 + 2, moltiplico sopra e sotto per √3 − 2, perché così sotto ottengo √3² − 2² che si può risolvere.
- Se al denominatore ho √2 − √3, moltiplico sopra e sotto per √2 + √3, perché così sotto ottengo √2² − √3² che si può risolvere.
- Se al denominatore ho 5 − √3, moltiplico sopra e sotto per 5 + √3, perché così sotto ottengo 5² − √3² che si può risolvere.
E così via…
^
Torna su
Forma esponenziale dei radicali
L'estrazione a radice è l'operazione inversa dell'elevamento a potenza; per questo motivo, ogni radicale può esser visto come una potenza ad esponente invertito
Tutte le proprietà delle potenze possono esser applicate quindi anche ai radicali, anzi possiamo integrare le proprietà di entrambe le operazioni, ad esempio:
Tale risultato lega le frazioni alle radici: ad esempio la proprietà invariantiva dei radicali vista inizialmente corrisponde alla proprietà invariantiva delle frazioni.
Inoltre tale proprietà spiega in modo automatico molte regole dei radicali viste prima.
Svolgere moltiplicazioni, divisioni e potenze tra radicali aventi lo stesso radicando è molto più facile se scriviamo i radicali in forma esponenziale.
|
Esempio 13. Svolgiamo la seguente espressione utilizzando la forma esponenziale.
√ 2 ·
(⁵√ 2 )3 ∶
(³√ 2 )4 ·
⁵√ 2 =
= 2 1 / 2 ·
2 3 / 5 ∶
2 4 / 3 ·
2 1 / 5 =
= 2 (1 / 2) + (3 / 5) − (4 / 3) + (1 / 5) =
= 2 (15 + 18 − 40 + 6) / 30 =
= 2 − 1 / 30 =
= 30√ ½
|
^
Torna su
<<< Precedente -
Successivo >>>
|
